¿Qué es un polígono?
La palabra polígono procede del griego antiguo πολύγωνον (polýgonon), de πολύ (polí)"muchos" y γωνία (goná) "ángulo".
¿Cuáles son los elementos de un polígono?
Una característica de los polígonos regulares, es que se pueden trazar inscritos en una circunferencia que tocará cada uno de los vértices del polígono. A medida que crece el número de lados de un polígono regular, su apariencia se asemeja cada vez más a la de una circunferencia.
En un polígono regular podemos distinguir:
- Lado, L: es cada uno de los segmentos que forman el polígono.
- Vértice, V: el punto de unión de dos lados consecutivos.
- Centro, C: el punto central equidistante de todos los vértices.
- Radio, r: el segmento que une el centro del polígono con uno de sus vértices.
- Apotema, a: segmento perpendicular a un lado, hasta el centro del polígono.
- Diagonal, d: segmento que une dos vértices no contiguos.
- Perímetro, P: es la suma de la medida de su contorno.
¿Cuáles son las propiedades de los polígonos?
Dadas las características de los polígonos regulares, podemos diferenciar algunas propiedades que se dan siempre, y que son de gran utilidad para determinar sus propiedades, y dimensiones geométricas.
- Los polígonos regulares son equiláteros; todos sus lados tienen la misma longitud
- Todos los ángulos interiores de un polígono regular tienen la misma medida, es decir, son congruentes
- El centro de un polígono regular es un punto equidistante de todos los vértices del polígono
- Los polígonos se pueden dividir en triángulos cuyos lados son el lado del polígono y los dos segmentos que unen el centro y los vértices (radios)
- El apotema es el segmento que une el centro y la mitad de cada lado del polígono
- El radio es el segmento que une el centro y cada vértice
Todos los polígonos tienen tres o más lados.
¿Qué son los ángulos de un polígono y de cuáles son sus respectivas fórmulas?
Ángulos centrales
- Todos los ángulos centrales de un polígono regular son congruentes y su medida α puede obtenerse a partir del número de lados n del polígono
en grados sexagesimales
Ángulos interiores
- El Ángulo interior,
, de un polígono regular mide:
en grados sexagesimales- Ángulos exteriores
- El Ángulo exterior,
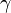, de un polígono regular es de:
en grados sexagesimales
- El Ángulo exterior,
